Selecting optimal models and hyper-parameters is crucial for accurate optic-flow estimation. This paper solves the problem in a generic Bayesian framework. The method is based on a conditional model linking the image intensity function, the unknown velocity field, hyper-parameters and the prior and likelihood motion models. Inference is performed on each of the three-level of this so-defined hierarchical model by maximization of marginalized a posteriori probability distribution functions. In particular, the first level is used to achieve motion estimation in a classical a posteriori scheme. By marginalizing out the motion variable, the second level enables to infer regularization coefficients and hyper-parameters of non-Gaussian M-estimators commonly used in robust statistics. The last level of the hierarchy is used for model selection. It expresses the conditional and direct dependance of the likelihood and prior motion models to the image data. The method is evaluated on image sequences of fluid flows and from the ``Middlebury" database. Experiments prove that applying the proposed inference strategy yields better results than manually tuning smoothing parameters or discontinuity preserving cost functions of the state of the art methods
References:
P. Héas, C. Herzet, E. Mémin. Bayesian inference of models and hyper-parameters for robust optic-flow estimation. IEEE transactions on Image Processing. 21(4):1437 -1451, 2012
P. Héas, C. Herzet, E. Mémin. Robust optic-flow estimation with Bayesian inference of model and hyper-parameters, Scale Space Methods and Variational Methods (SSVM) in Computer Vision, Israel, June 2011.




Dimetrodon image sequence. Frame 10 of the “Dimetrodon” sequence and motion ground truth in color visualization [Baker07]. In the latter visualizations, color and intensity code vector orientations and magnitudes.

Model selection and hyper-parameter inference. Selection of the most likely norms for the data and the regularization terms. Hyper-parameters estimates (regularization coef. “gamma” & robust data “tau_d” and regularization “tau_r” parameters) and score of the different norm associations in terms of marginalized likelihood probability, end point and Barron angular error. The model association probalility is minimized for the likelihood f_d= (OFC model with L1 norm) and for the prior f_r= (1-st order regularizer with L1 norm). The selected models also minimize the end point and the angular average errors.
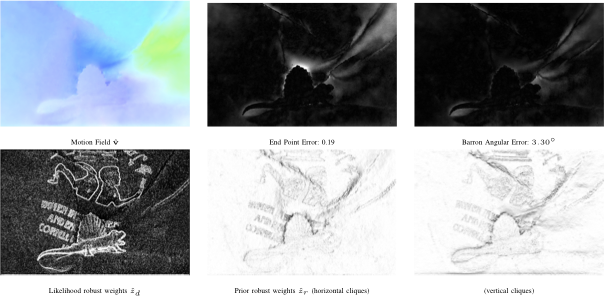
Performance of motion estimation. Color visualization, end point and Barron angular error maps of the motion estimate obtained with the selected models (OFC data model and first order regularizer with L1 norm) and the inferred hyper-parameters. The bottom row displays spatial maps of robust weights and corresponding to the inferred M-estimator hyper-parameters.

Simulated scalar diffusion by 2D turbulence. Generated scalar image and ground truth motion field visualization in a vectorial and in a color representation.

Influence of hyper-parameter tuning and model selection on motion estimation performance. DMotion estimates, End point and Barron angular error for different settings of data model and hyper-parameters (The data model is defined by the diffusion coefficient “sigma” driving the scalar diffusion). The regularization coefficient “gamma” and the robust parameter “tau_d”